PN结原理与二极管特性全解析|半导体器件基础图文指南
一、势垒电容 vs 扩散电容
1.1 势垒电容(Depletion Capacitance)
形成原理
-
物理本质:空间电荷区(耗尽层)的电荷量随外加电压变化产生的电容效应
-
微观过程:
- 反向偏压增大 → 耗尽层变宽 → 更多电离的施主/受主离子暴露 → 存储电荷量增加
- 反向偏压减小 → 耗尽层变窄 → 部分离子被载流子中和 → 存储电荷量减少
数学描述
$$
C_T = \frac{\varepsilon A}{W(V)} = \frac{C_{T0}}{\sqrt{1 - V/\phi_0}} \quad (反向偏压时)
$$
-
( \varepsilon ): 半导体介电常数
-
( A ): PN结面积
-
( W ): 耗尽层宽度(随反向电压( V )变化)
-
( \phi_0 ): 内建电势(Si约0.7V)
特性对比
| 工作区域 | 电容值范围 | 应用实例 |
|---|---|---|
| 反偏 | 1~100pF | 变容二极管调谐电路 |
| 零偏 | 最大(无电场) | ESD保护设计 |
类比理解:
将耗尽层视为一个可伸缩的"电荷仓库",电压变化相当于改变仓库容积:
- 反向电压增大 → 仓库拉长(存储更多离化离子)→ 单位长度电荷密度降低 → 等效电容减小
1.2 扩散电容(Diffusion Capacitance)
形成原理
-
物理本质:正向偏置时,非平衡少子在扩散过程中形成的电荷存储效应
-
微观过程:
- 正向电压升高 → P区空穴注入N区成为少子 → N区少子浓度梯度增加
- 这些少子需要时间扩散到深处(少子寿命( \tau ))→ 电荷积累形成电容
数学描述
$$
C_D = \frac{\tau I_F}{V_T} \quad (正向偏压时)
$$
-
( \tau ): 少子寿命(Si约1μs)
-
( I_F ): 正向电流
-
( V_T ): 热电压(26mV@300K)
特性对比
| 工作区域 | 主导因素 | 典型值 |
|---|---|---|
| 正偏 | 少子浓度梯度 | 100~1000pF |
| 反偏 | 可忽略 | <1pF |
类比理解:
想象给水箱注水(注入少子):
- 突然打开水阀(电压升高)→ 水位需时间达到稳定(电荷积累)
- 关闭水阀(电压降低)→ 水位缓慢下降(少子复合)
二、雪崩击穿机制详解
2.1 物理过程
-
强电场加速:反向电压使耗尽层电场强度( E )超过临界值(~3×10⁵ V/cm)
-
碰撞电离:高能载流子撞击晶格原子 → 产生新电子-空穴对
-
链式反应:新生载流子被加速 → 进一步电离 → 电流指数级增长
2.2 低掺杂浓度要求
-
数学条件:
$$ E_{max} = \frac{qN_D W}{\varepsilon} \quad (N_D为掺杂浓度) $$- 低掺杂 → 耗尽层宽度( W )大 → 相同电压下电场强度低 → 需要更高电压达到临界电场
-
设计意义:低掺杂PN结能在更高电压下才发生雪崩击穿
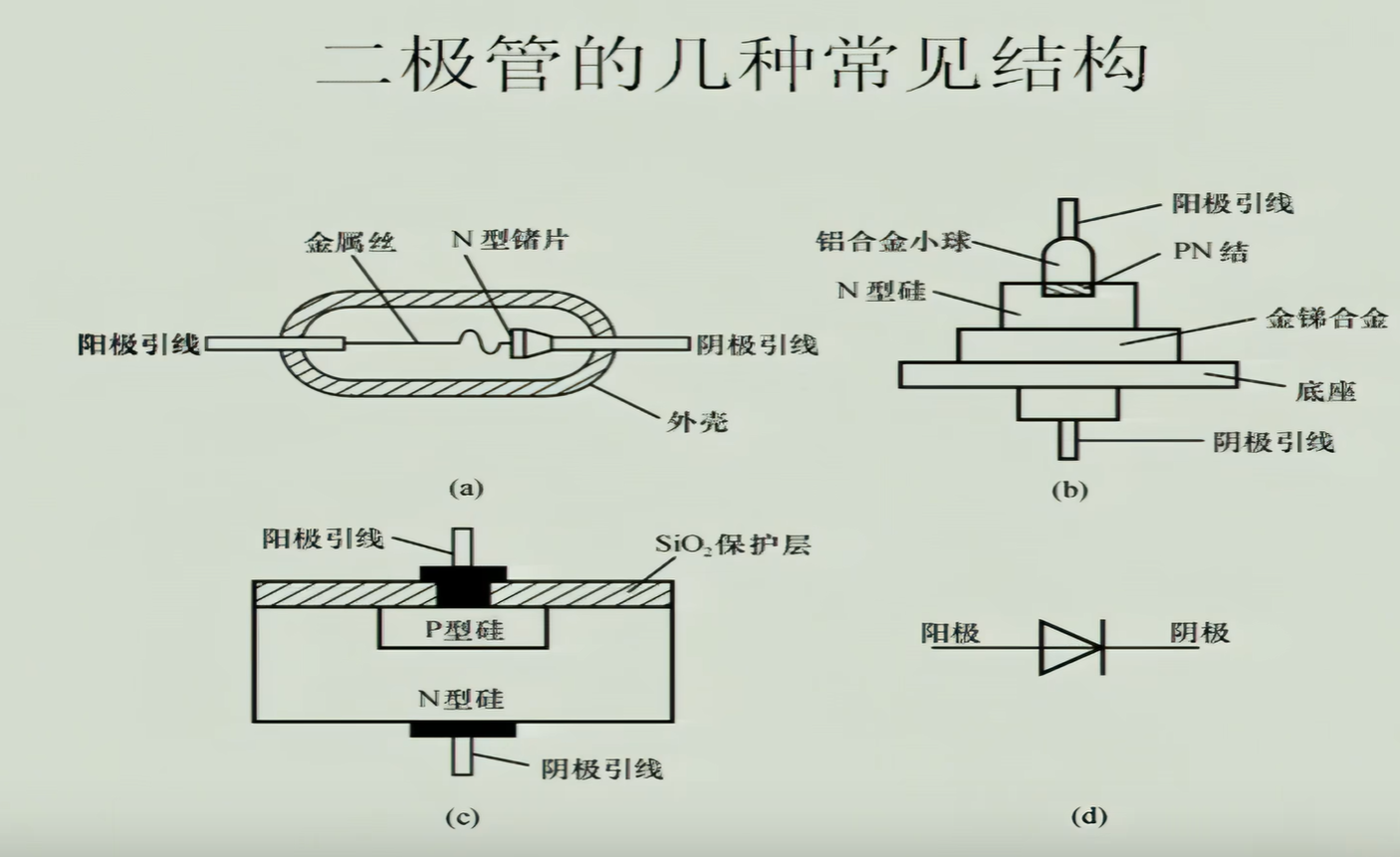
三、半导体二极管结构与伏安特性
3.1 二极管结构类型
1. 点接触型二极管
1 | 金属触针(阳极) |
-
特点:结面积小(≈μm²),结电容极低(0.1~1pF)
-
应用:高频检波(如收音机中的1N34)
2. 面接触型二极管
1 | 金属阳极 |
-
特点:结面积大(≈mm²),允许大电流(>1A)
-
应用:电源整流(如1N4007)
3. 平面型二极管
1 | 金属电极 |
-
特点:可精确控制结深,反向恢复时间短(≈ns级)
-
应用:高速开关(如1N4148)
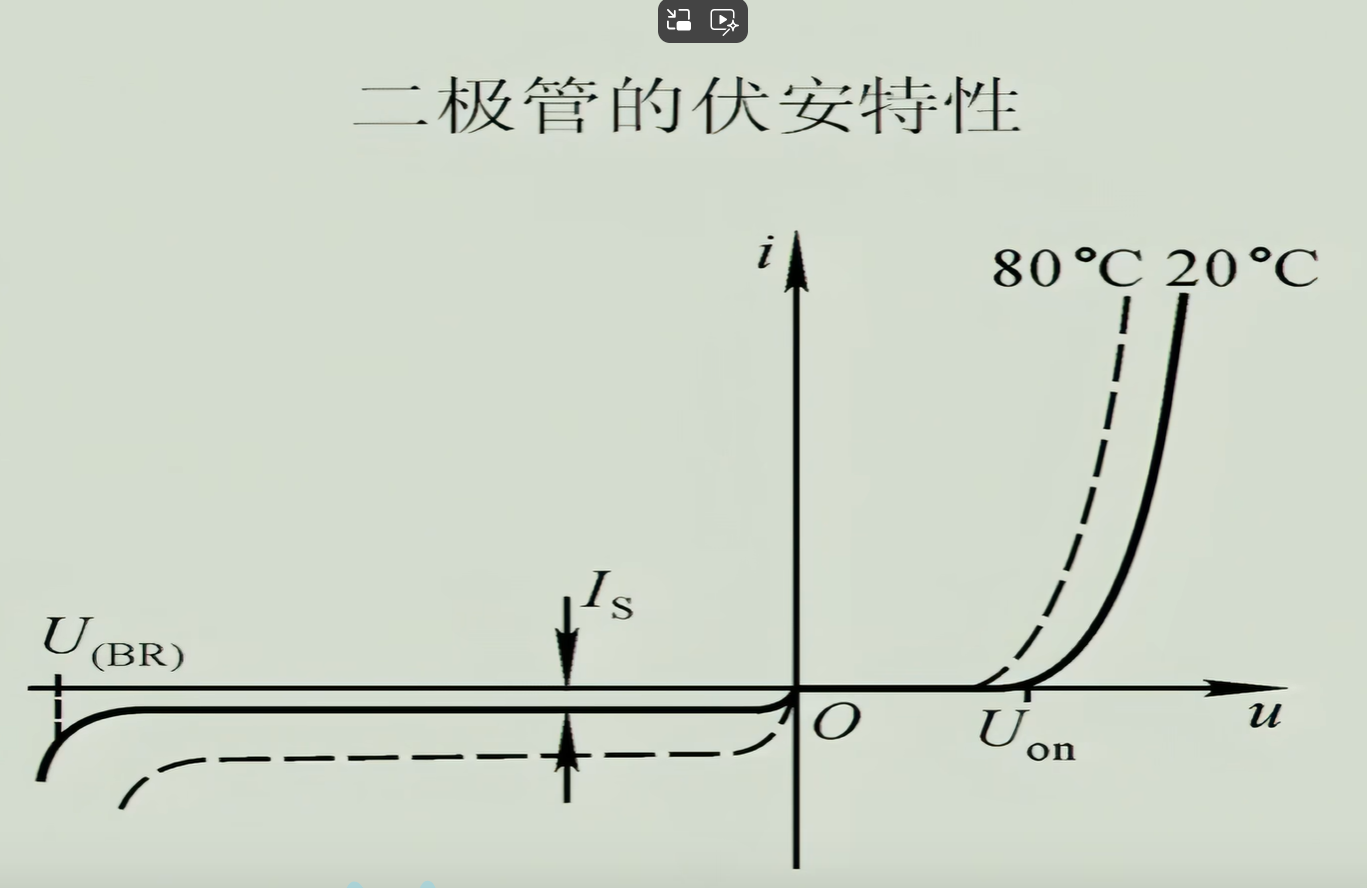
3.2 伏安特性曲线详解
1 | I(mA) |
分区域解析
-
死区(0 < V < V_th)
- 物理机制:外电场未克服内建电场((E_{ext} < E_{in}))
- 电流方程:
$$
I \approx I_S \left( e^{V/(nV_T)} -1 \right) \approx 0 \quad (V < 0.5V)
$$
-
指数增长区(V_th < V < 0.7V)
- 载流子行为:多子扩散主导,复合减少
- 数学描述:
$$
I = I_S e^{V/(nV_T)} \quad (n=1\text{理想},实际n≈1.2)
$$
-
线性区(V > 0.7V)
- 限制因素:体电阻(R_s)(P/N区材料电阻)
- 特性方程:
$$
I = \frac{V - V_{th}}{R_s} \quad (R_s≈0.1Ω~\text{典型值})
$$
四、雪崩击穿与掺杂浓度关系
4.1 雪崩击穿的定量分析
临界电场条件
雪崩击穿发生的临界电场强度 ( E_{\text{crit}} ) 由材料决定(对硅约为 ( 3 \times 10^5 , \text{V/cm} ))。
耗尽层宽度与掺杂浓度和反向电压的关系为:
$$
W = \sqrt{\frac{2 \varepsilon (V_{BR} + \phi_0)}{q} \left( \frac{1}{N_A} + \frac{1}{N_D} \right)}
$$
推导逻辑:
-
耗尽层总电荷量需满足电中性:( N_A W_p = N_D W_n )
-
总耗尽层宽度:( W = W_p + W_n )
-
泊松方程积分得到电场分布,最大电场发生在界面处
当掺杂浓度 ( N_D ) 较低时:
-
耗尽层宽度 ( W ) 增大
-
相同反向电压下,平均电场强度 ( E_{\text{avg}} = V_{BR}/W ) 降低
-
为达到临界电场 ( E_{\text{crit}} ),需要更高的击穿电压 ( V_{BR} )
击穿电压公式
对单边突变结(如 ( N_A \gg N_D )):
$$
V_{BR} \propto \frac{1}{N_D}
$$
设计意义:
-
低掺杂 → 高击穿电压(适合高压二极管)
-
高掺杂 → 低击穿电压(适合稳压二极管)
五、二极管伏安特性曲线的温度依赖性
5.1 正向特性的温度效应
-
阈值电压降低:
$$
\frac{\partial V_{th}}{\partial T} \approx -2 , \text{mV/°C} \quad (\text{硅})
$$- 原因:禁带宽度 ( E_g ) 随温度升高而减小
- 对电路的影响:恒压源供电时,温度升高会导致电流显著增大
-
体电阻变化:
$$
R_s(T) = R_{s0} [1 + \alpha (T - T_0)]
$$- 硅的电阻温度系数 ( \alpha \approx 0.07 , \text{/°C} )
- 高温时体电阻增大,线性区斜率减小
5.2 反向特性的温度效应
-
反向饱和电流激增:
$$
I_S(T) = I_{S0} \left( \frac{T}{T_0} \right)^{3} e^{-E_g/(kT)}
$$- 每升高 10°C,( I_S ) 约增大 1 倍
- 对高温电路的威胁:漏电流可能引发误动作
-
击穿电压变化:
- 雪崩击穿:正温度系数(( +0.1%/°C ))
- 齐纳击穿:负温度系数(( -0.05%/°C ))
六、二极管典型应用与选型指南
6.1 应用场景与结构匹配
| 应用场景 | 推荐二极管类型 | 关键参数要求 | 代表型号 |
|---|---|---|---|
| 高频检波(>100MHz) | 点接触型 | 结电容 < 1pF | 1N34 |
| 电源整流(50Hz) | 面接触型 | 最大电流 > 1A | 1N4007 |
| 高速开关 | 肖特基二极管 | 反向恢复时间 < 10ns | BAT54 |
| 电压基准 | 齐纳二极管 | 稳压精度 ±5% | BZX55C5V6 |
6.2 选型参数速查表
| 参数 | 点接触型 | 面接触型 | 肖特基二极管 | 齐纳二极管 |
|---|---|---|---|---|
| 最大反向电压 | 50V | 1000V | 40V | 3-200V |
| 最大正向电流 | 50mA | 3A | 1A | 5mA |
| 结电容 | 0.5pF | 50pF | 100pF | 50pF |
| 反向恢复时间 | 1ns | 1μs | <10ns | 1μs |